數學從解決問題中產生，並在解決各種問題的過程中不斷發展起來。數學的真正組成部分是『問題』和『解』；解題也是數學學習過程的一個重要部分。今天的社會，繁複的計算工序絕大部分由計算機和電腦進行。因此，新的課程指引建議減少無謂的計算操練，將時間多投放在提升學生的解難能力（課程發展議會，2002）。

第三屆國際數理學習研究結果顯示，香港小學生的平均數學能力不差，在 26 個國家／地區中排行第四位。看似我們應該感到高興，但排行首三位的卻是日本、新加坡和南韓，而且中國並沒有參與是次研究，可想像得到，香港小學生的平均數學能力在亞洲區算是落後的。

梁、容和杜（2002）在其報告指出，香港學生一般強於運算和解決常規問題。究其原因是學生多做習作，反覆操練。但在處理非常規問題時，香港學生則表現較差，反映香港學生欠缺解難能力的培養。

現時香港小學生大部分能掌握基本運算和解決簡單文字題，他們欠缺的是解決難題時的思考方法。要培養學生的解難能力，須讓他們掌握解難過程和靈活運用解難策略。如果要進行解難教學，協助學生理解及掌握解難過程是必然之事。

解難過程
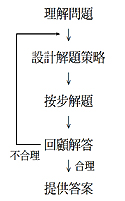
解難是一個過程，從解題者開始接觸問題，經過處理已知資料，最後找到答案或結論並作出回顧為止。學生須充分掌握這個過程，才能有效解決學習時遇到的常規及非常規問題。

Polya（1945）在他影響深遠的經典著作「How to Solve It」《如何解題》指出解難過程可分為四個階段：
1. 理解問題（Understanding the problem）
2. 設計解題策略（Devising a plan）
3. 按步解題（Carrying out the plan）
4. 回顧解答（Looking back）

繼Polya之後，也有幾位學者為解難引入不同模式，包括Krulik and Rudnick（1988）的模式：理解（Read）、探索（Explore）、選取策略（Select a strategy）、解決（Solve）和回顧及延伸（Look back and extend）。

雖然這些解難模式的重點各有差異，它們的最終目標都是提升學生的數學思維，在解決難題時能夠有系統地進行。以Polya的模式為例，老師可以用以下提問協助學生進行解難的四個階段：

理解問題（Understanding the problem）
‧你明白問題的每字每句嗎？
‧你能否用自己的文字重述問題？
‧已知量和未知量是甚麼，它們的關係如何？
‧目的是甚麼？
‧資料足夠嗎？
‧有沒有哪些資料是不相關的？
‧這個問題「難」在哪裡？
在這個階段，鼓勵學生反覆讀題，找出有用資料和問題重心。

設計解題策略（Devising a plan）
‧這個問題是否跟曾解決過的問題類似？
‧可否用另一種型式表達？
‧可否試以較簡單情況替代？
‧可否用另一種形式表達有用資料？

在這個階段，鼓勵學生思考能否直接運用定理、公式等解題。如果不能，鼓勵他們將資料用圖／表顯示，或試解較簡單問題，在得到新的靈感後，選取較適合的策略再進行探究。小學生常用的策略有很多，包括：
‧估猜與測試（Guess and Test）
‧繪圖（Draw a picture）
‧探索規律（Look for a pattern）
‧解一簡化問題（Solve a simpler problem）
‧應用數目的性質（Use properties of numbers）
‧逆轉思考（Work backward）
‧窮盡可能性（Exhaust possibilities）
‧尋找公式（Look for a formula）
‧應用工具（Use tools）
‧推理（Reasoning）
‧進行模擬（Do a simulation）
‧應用變量思考（Use a variable）

按步解題（Carrying out the plan）
‧你是否想出了一個解題方法嗎？
‧能否依這個方法計算下去？

在這階段，鼓勵學生應用並執行所選用的計劃，直至獲得解答或更明確的新解題方略。 宜提醒學生給自己合理、充份的時間去思考，若不成功可從別處尋找線索又或將問題放下一回再思考。並不要害怕重新開始，很多時候，新的開始，新的策略會導致成功。

回顧解答（Looking back）
‧這個答案正確嗎？
‧這個方法正確嗎？
‧為甚麼用這個方法可得出正確答案？
‧有哪些關鍵步驟？
‧這方法能應用到類似的問題嗎？
‧有沒有其他方法？
‧如果有其他方法，何者較佳、較快或較易於概括？
‧如果問題的條件改變了，情況又會怎樣？

在這階段，鼓勵學生驗算，並須指出驗算不是將答案代入公式，而是檢視答案能否滿足題目內容及要求。另一方面，可鼓勵學生思考其他解題方法及將問題延伸，以增強其探究能力（梁志強，2003）。

如果學生解題時正確理解問題，下圖反映回顧時發現答案合理或不合理後的流程。

我們嘗試用以下例子分析解難四個步驟可能出現的情況。

題目：有大、小正方形手帕各一塊置於面積是900平方厘米的花紙上。兩塊手帕的邊長相差 4 厘米，面積相差 56平方厘米。大手帕的面積是多少？

在理解問題的階段，學生須清楚指出：
有用的資料
‧手帕是正方形的
‧一大、一小共有兩塊
‧邊長相差 4 厘米
‧面積相差 56 平方厘米
題目的要求
‧大手帕的面積是多少？
沒用的資料
‧花紙的面積是 900 平方厘米

面對這樣的題目，學生可視乎個人的數學知識和解題經驗來設計解題策略。以下是解決此題的其中五個方法：

方法一：代數式

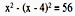
具備中學或以上的數學知識的人，大多會用代數式來解決此題。但對小學生來說，這是一道難題，因為他們未能理解當中代數符號的運算。面對這樣的難題，他們可以怎樣解決？

以下是一些小學生可能運用的解題方法：

方法二：繪圖

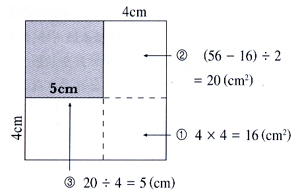
教學提問：
- 題目中提供了哪些資料？
- 這裡有多少個正方形？當中哪些是有關係呢？
- 怎樣利用已知的資料去找出兩個正方形的大小？
- 正方形的面積與邊長有甚麼關係？
- 試試畫圖看看。
- 該怎樣畫圖才能清楚表示出題目提供的資料？
- 如何可以以一幅圖顯示這兩個正方形的關係呢？
- 把兩個正方形重疊擺放有甚麼好處？
- 透過畫圖，你們找到新的資料嗎？
- 透過畫圖，你找到甚麼新資料？
- 怎樣利用這些資料去找出大、小正方形的面積？

方法三：列表與試誤 I

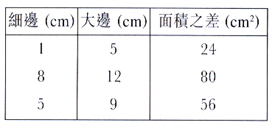
教學提問：
- 題目中哪些資料可以讓你作初步嘗試？
- 這次嘗試能滿足題目的所有條件嗎？
- 如果未能夠滿足所有條件，可以怎樣做呢？

方法四：列表與試誤 II
教學提問：
- 大正方形的面積最少是多少？

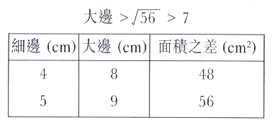
方法五：列表與觀察規律

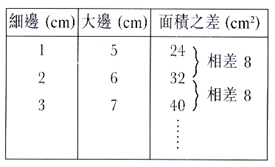
- 每條邊增加 1 cm 後，面積之差有甚麼改變？
- 改變有沒有規律？
- 每邊要增加多少才能滿足題目的要求？
- 所以，小正方形的邊長是多少？

學生按上述方法進行計算，如果沒有出現錯誤，會獲得大手帕的邊長為 9 厘米。

答案合理嗎？在回顧時，學生須驗算兩塊手帕的邊長是否相差 4 厘米和面積是否相差 56 平方厘米。最後才寫下答案：大手帕的面積為 81 平方厘米。

結論
掌握解難過程是解決數學難題的基本功。本文用了一個例子描述解難過程的四個階段，並建議教學時在每階段用提問來激發學生思考。

面對一個不熟悉的問題，第一步當然是先理解問題，找出問題核心和有用資料。第二步是想出一個可以解決問題的方法，如果找到直接解題的數學方法，那就直接使用吧；否則，便要想想有哪些解難策略可以幫忙了。有了解決問題的方法，便執行吧，這是第三階段。終於找到答案了，它能滿足問題的已知條件和要求嗎？這須要驗算啊！還有其他答案和方法嗎？在這第四階段，學生可以發展自我肯定和繼續探究的能力。

如果學生認真審題，他們在理解問題時應沒有太大困難。較大的挑戰是如何設計解難策略。發展本地小學生解難策略的參考書籍甚少，在優質教育基金贊助下，梁、林、潘、文和王（2005）就著小學四年級發展一套教材，協助小四學生掌握解難過程和建立六種常用策略，包括：試誤、繪圖、列表、窮盡可能性、逆轉反思和觀察規律。該套教材曾經在十間學校試用，學生和老師的回應令人鼓舞。如果數學老師希望培養學生的解難能力，該教材套或能提供一些實用的材料。