現今社會發展迅速,科技一日千里,資訊爆炸,經濟急速轉型,為使我們的學生有能力應付未來社會日新月異的急劇改變與挑戰,香港課程發展議會於二○○一年六月公布了《學會學習——課程發展路向》,其中指出發展學生共通能力的重要性,從強調知識的灌輸轉為著重學生「學會學習」、懂得如何思考及解決問題。課程改革也從以往只偏重學術的研習,轉為強調多元化的全人發展。
九種共通能力的其中一種是解決問題的能力,提升學生解決問題的能力,不但是現今教學的重點工作之一,也是現代數學教育的重要發展方向。因此,提升學生解決問題的能力實為家長、教師與學生三方面的共同願望。但我們應從哪裡起步?應做甚麼?應怎樣做?哪些地方要加強?哪些問題應避免?……這些問題都使人感到困擾,但教師又不能不深思熟慮,作出針對性的課程策畫和調節教學工作,以達到提升學生解決問題的能力。
「知彼知己,百戰百勝。」教師必須先了解學生有甚麼困難,才能收到良好的教學效果。現略述學生常遇到的困難如下:
- 對某些數學語言未能掌握,或因語文程度不及而未能理解題意。
- 未能掌握數量關係。
- 未能有效地運用思考工具,以協助他們分析重點及解決問題。
- 認識解決問題的步驟,及切實嘗試按步地解決問題。
- 欠缺一般解決問題策略的知識,甚至從未接觸過非常規的問題。
- 由於上述的不足,一般學生對問題都有恐懼感,部分學生更因欠缺自信心而導致對數學不感興趣。
解決學生上述的各種困難,非三言兩語可說得清楚,各校學生的能力和興趣都不同,學生的個別差異情況也非一致。因此,各學校宜因應該校的需要,來擬定校本解難的教學策略,以下是其中一些可提升學生解決問題能力的建議:
甲、 |
強調數據關係及協助學生掌握與各學習範疇有關的數學語言及概念
比較以下兩個數據:
甲有 80 元 乙有
60 元
以下是一些描述以上的數據關係的例子:
1) 甲有的款項比乙的多 20
元
2) 乙有的款項比甲的少 20
元
3) 甲有的款項是乙的 1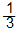
4) 乙有的款項是甲的 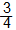
5) 甲有的款項比乙的多 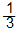
6) 乙有的款項比甲的少 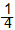
7) 甲有的款項比乙的多 33.3%
8) 乙有的款項比甲的少 25% |
以上的描述是學生經常不能理解,但又常常在數學問題中出現的數學語言。因此,教師必須使學生清楚理解:哪一個數量較多?多了多少?在比較甲、乙兩個數據時,必須知道哪一個數據是用作比較的依據?哪一個可用作分母?哪一個用作分子……等。在數學語言的運用上,教師還需要看看學生是否能正確地運用數學符號,及有關「度量」、「圖形與空間」和「代數」等概念。
乙、建構正確的加、減、乘、除等的概念
常聽到很多教師說,學生的計算題成績很好,但對應用題或開放題目則束手無策。
事實上,初小的「加法」、「減法」及「加和減的關係」;「乘法」、「除法」及「乘和除的關係」都是重要的課題,不容輕視。例如:
加法概念如添加、合併、改變、比較;
減法概念如改變、取去、比較;
乘法概念如同數連加、倍、率;
除法概念如連減、均分、包含……等。
這些概念都應在初小時明確地介紹清楚。至於加、減、乘、除法的題型很多,本文不準備詳作介紹,但筆者想請讀者比較下面兩題:
| 小一題目: |
小明有
3 塊餅,家希有的餅比小明多
2 塊。兩人共有餅多少塊? |
| 小六題目: |
小明有 28.5
元,家希有的款項比小明多
15.7 元,兩人共有多少元? |
從上述兩題常規應用題中,我們不難發現它們所涉及的數理完全相同,只是數據不同而已。數學課程雖然是以螺旋式推進,但若學生在低年級時的基礎學得不好,必會影響他們在高年級的學習。
部分教師認為初小的數學課程太淺,不會花時間與學生多做活動和討論。部分學校更有偏見地選派數學教學能力較弱的老師,任教低年級數學科,此舉實屬不智。
正確的數學概念是需要學習者自己建構的,教師可以透過有趣的活動或遊戲等形式,以數學教學重點為主幹,實物教具或電子教具等資源為輔助,引導學生透過具體的操作,探索數學世界。(參看圖例(一))
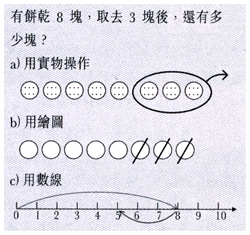 圖例(一)減法活動
圖例(一)減法活動
(1)從數的分裂(分解)與組成(合成)到加減關係
「數」範疇佔小學數學課程中一個極大的比重。小一課題中有「數的分裂與組成」,這是學生正規地學習加法和減法之前的準備階段。
學生要從具體的實物操作、圖畫表達、反復活動及初步探索這些數據關係與加減關係。(參看圖例(二))
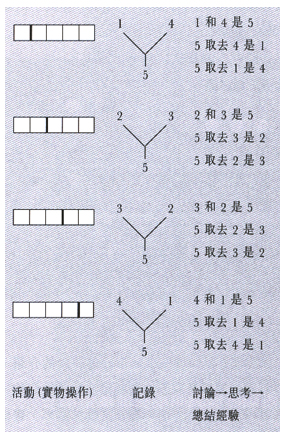 圖例(二) 圖例(二)
另一階段的學習是透過實物操作,讓兒童理解及懂得用不同的方法去描述數量關係。英國數學教育家利碧嘉(P.
Leibeck)認為兒童學習數學的認知程序,可以概括為經驗(Experience),語言(Language),圖像(Picture)和符號(Symbol)四個環節。由此可見兒童學習數學,應透過活動、體驗及觀察事物去建構數學概念。同時,更要把文字、語言和有關的事物或情境連結及配合,以達到理解及掌握有關的數學語言。例如:排棋子活動(參看圖例(三))
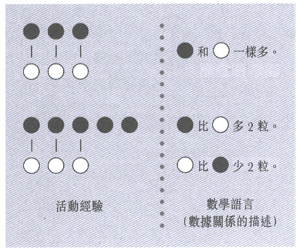 圖例(三)
圖例(三)
隨著「+」、「-」、「=」等符號的介紹,該等數量關係及有關加法和減法的活動經驗,亦可以由下列右方的幾題算式總結起來,建構加減的運算是互逆的概念。(參看圖例(四))
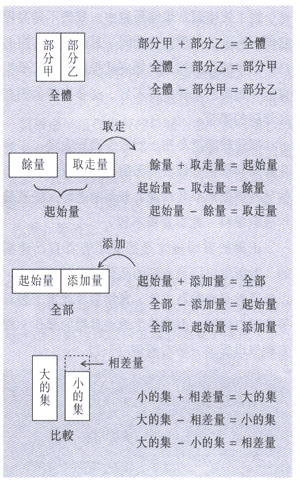 圖例(四)
圖例(四)
以上為一般加減法的題型結構,每一題型都涉及三個數量。至於應該用加法或減法去解決問題,則視乎三個數量中哪一個是未知數。
學生經過足夠的活動或實際情境的體驗,可以用言語來描述,並且在腦海中形成圖像,再概括成上面的算式,建構加和減的運算是互逆的概念。
(2)由數的分解與合成到乘除關係
我們也可以從數的分解與合成理解乘和除的關係,對於不含 0
的數據,乘和除是互為逆運算的。
a)
數量的乘積(Product
of Measures)
3
和 4
相乘中,3 和 4
是因數,12 是積。
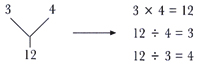
日後進一步的學習亦以上述概念為基礎。例如:
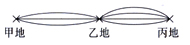
由甲地至丙地共有 (3 x 4)
條路徑。
b) 乘法概念中的同數連加、倍或率與等分除法和包含除法的關聯在於數量的同構(Isomorphism
of Measures)。例如:
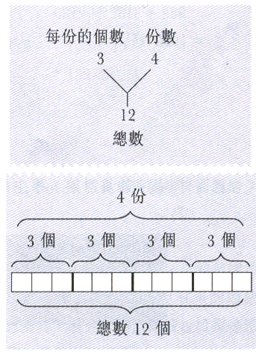
經過活動及討論,學生總結經驗為:
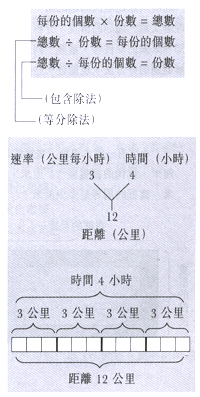
經過活動及討論,學生總結經驗為:
速率 x 時間
= 距離
距離 ÷
時間 = 速率
距離 ÷
速率 = 時間
丙、提供思考工具
理解問題是解決問題的第一個步驟,這包括理解文意、問題的情境、分析問題的核心、已知和未知的條件等。畫圖、列表等都是有助理解問題的好方法。現簡述一些解決問題的方法:
1) 圖解
小明有一個木畫框,畫框的每邊闊
10 厘米。框內的圖畫長 74
厘米,闊 35 厘米。畫框的周界是多少厘米?
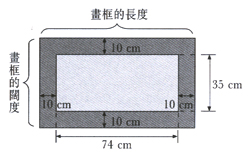
畫框的長是:74
+ 10 + 10 = 94(厘米)
畫框的闊是:35 + 10 + 10 = 55(厘米)
畫框的周界是:(94 + 55) x 2 =
298(厘米)
根據題意畫圖,再標示出提供的數據,畫框的長度和闊度是否已一目了然呢?有了找出答案所需的條件
—— 畫框的長度和闊度,便可解決問題了。
2)
線段圖
海洋館內有小丑魚 982 條,孔雀魚比小丑魚多
3150 條,而神仙魚比孔雀魚少
2180 條。海洋館內有神仙魚多少條?
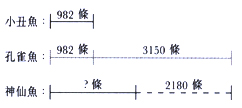
海洋館內有神仙魚:
982 + 3150 - 2180
= 1952(條)
3)
表列
小狗重 6 公斤,小貓比小狗輕
2 公斤,牠們共重幾公斤?

牠們共重: 6 + 6 - 2
= 10(公斤)
4)
樹狀圖
水果店有 80 個橙,120
個蘋果和 60 個梨,楊桃的數量是蘋果和橙數量的和,菠蘿比楊桃少
75 個,有菠蘿多少個?
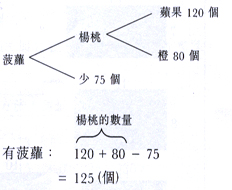
丁、執行 G.
Polya 所提出四個解決問題的步驟:
(1) |
弄清問題
分析題目:問的是甚麼?已知數據是甚麼?條件是否充分?有沒有多餘的數據?以圖解、表列、樹狀圖或線段圖等思考工具,協助弄清問題。 |
(2) |
擬定解決問題的計畫
利用已知數據與未知數據的關聯,或簡化問題等方法,擬定解決問題的計畫。 |
(3) |
執行計畫 |
(4) |
回顧 |
驗算及看看有沒有其他可行的解法。 戊、建立解決問題的策略
解決問題的策略有很多,本文不能盡述,但一般適用於小學生的有以下幾種:
(1)簡化問題
(2)簡化數據
(3)試誤或猜想
(4)尋找規律
(5)倒推思考
(6)表列
(7)代數
(8)實驗與模擬
現以下列問題作例子,闡述有關解決問題的策略:
例一:
小明用一條長 40
厘米的繩子圍出一個長方形,長方形的長和闊分別可能是多少厘米?(各答案在整數範圍)
先分析:
- 問題的目的是甚麼?
(要找出長方形的長和闊分別可能是多少厘米)
- 已知數據是甚麼?
(周界是 40 厘米)
- 已知數據和未知數據有甚麼關係?
((長 + 闊)x 2 =
周界)
方法一:表列
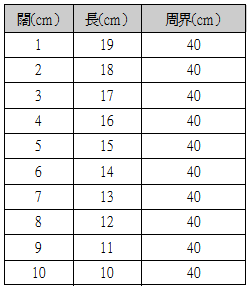
方法二:圖解
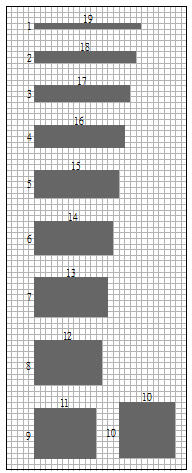
方法三:倒推思考
| 因為: |
長方形的周界 = (長 + 闊)x
2 |
| 這表示: |
長 + 闊 |
= 周界
÷ 2 = 40 ÷ 2 |
| |
= 20(厘米) |
| 所以: |
長 + 闊 = 20
厘米 |
在整數範圍中,兩數的和是 20
的算式有:
| 10 +
10 = 20 |
15 +
5 = 20 |
| 11 + 9 = 20 |
16 + 4 = 20 |
| 12 + 8 = 20 |
17 + 3 = 20 |
| 13 + 7 = 20 |
18 + 2 = 20 |
| 14 + 6 = 20 |
19 + 1 = 20 |
利用以上方法,便可找到長方形可能的長和闊了。
例二:
213 加上 ______,結果可被
5 整除。
方法:猜想
比 213 大的「5
的倍數」有:
215、220、225、230、……
所以,答案可能是:
2、7、12、17、……
例三:
小怡有 100
元,想買以下三件不同的衣服,應找回多少元?
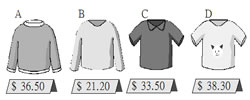
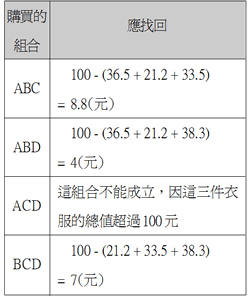
方法:列及試誤
先找出小怡可以買哪三件衣服,再看看應找回多少元。
己、提升提問技巧,著重啟發學生思考
教師的解決問題教學策略,重點並不在於如何教授,而在於如何啟發學生作多角度的思考、明確地弄清題意、理解數據的關係、增加課堂的互動性,讓學生自行建構解決問題的策略。
教師其中一個常犯的毛病,是未有給予學生足夠的時間思考,便急急作示範,鉅細無遺地把解決問題的方法向學生逐一解說,因為教得太多、說得太多,不但不能啟發學生的思考,只會扼殺了學生學習數學的興趣,剝奪了他們解決問題的機會,使他們只知模仿,不懂思考,更遑論提升他們解決問題的能力了。
教師宜盡力營造積極的討論氣氛,適當地利用標準及變式的例子,給予學生足夠的思考時間,多提出高層次思考性的問題,並積極跟進學生的問答,以引發進一步的討論及更深入的探究,藉以提升他們解決問題的能力。

參考資料
|
1. |
課程發展議會。《學會學習——課程發展路向》。香港:課程發展議會,2001
版。 |
|
2. |
G. 波利亞(George
Polya)著;閰育蘇譯。《怎樣解題》二版。台北市:九章出版社,1993。 |
|
3. |
John A. Van De Walle
著;張英傑,周菊美合譯。《中小學數學科教材教法》初版。台北市:五南圖書出版公司,2005。 |
|