「數學就是生活，生活就是數學。」在過去的日子，數學教育和日常生活應用的互動關係較弱。數學教育的重點，側重「理論」的演練和運算技巧的傳授，在數學應用，尤其在日常生活中的運用較少觸及。

在一九八零年，美國數學教育協會（NCTM）認同數學在日常生活應用的匱乏，於是倡議數學課程的改革；他們認為數學教育應該培養學生的高階思維能力、分析能力和創造能力，去明白數學；好等學生有備數學的內涵和適切的變通能力，去面對千變萬化的知識型社會和資訊爆炸的年代。其中一個主要的提案是在數學課程中滲入解難的能力。

既然得知解難在數學課程和教育的重要性，因此，「如何提升學生的解難的能力？」就值得我們深入去探究和討論。

解難的理念和認知
解難是引導學生，幫助學生解決疑難問題之過程和結果。解難的本質是一系列互相緊扣的活動。目的是去培養學生質疑的習慣和自學能力，藉以提高學生的分析力，從而體現問題的核心，最終將問題解決。主要解難的活動羅列如下：（見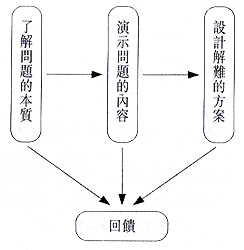圖一）

圖一

解難的技巧
提升解難能力的一個主要元素是演繹者（老師和學生）如何去分析問題，尋找最佳的路徑，使用適當的策略和技巧（程式），去體驗和解決問題。（見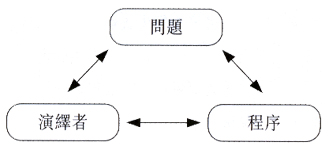圖二）

圖二

解難是一個不斷向前進行的程序，不是一個例行常規的活動；意思是說每一個步驟可以重新組合去得到最適切的路徑。同時，也可將不同策略運用於不同階段，將隱藏的引子顯示出來，令難題能夠有效地解決。下列例子會展示如何有效地去提升解難能力。

不同手法 同一答案
很多問題，都不會只有一個解決的方法。任何一個數學問題，都可以演化成一道簡單算術題、代數題，或幾何關係的問題，從而利用邏輯推理去尋找答案 。

因此，教授解難能力的方法，重點是建構學生的邏輯思維能力，去引探題目的癥結，尋找最適切的路徑，並不是將標準答案展示出來。

例一
九位客人參與一個宴會，每一位客人都會和其他客人握手，請問握手的次數總共有多少？

其中一個解題的方法，是利用模擬的方法，從一個小問題開始，之後利用圖表去歸納答案，直至找出數型為止。因此，此一道題的答案，可以歸納如下表。

當我們考慮第二行數字的差時，我們可以得出下列的結果：

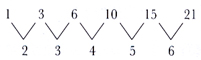
根據此一數型的發展，我們就可以得知以下兩數的答案為 2l + 7 = 28 和 28 + 8 = 36，而最後的答案為 36 + 9 = 45。

在教學過程中，老師必須提醒學生，可從多方面、多角度去思考每一道題，從而找出最合適的解決方法。在例一中，如果每次由一個客人起立和其他客人握手，學生可以計算得到總共握手的次數為 9 x 8 = 72。可是，此種握手方法會有重複的情況，就是當國華起立時會與華豐握手，當華豐起立時，會與國華握手；故此，當兩個人互相握手時，他們的握手情況就會重複計算。因此，真正的答案將會是 72 ÷ 2 = 36。

當老題延展學生的想法時， 他們可能利用數學演繹法去計算：當有 n 個客人時，握手的次數將會為：
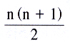                  n 為客人的數目

在此一情況下，學生就可以感受得到不同解題的經驗。當老師作出適當的指導，學生就可以學習得到和運用理性分析去找出題目的真相和遺忘的盲點。當日後遇到數學難題時，思考方法不會困於某一個起點之上。

設立挑戰問題、遊戲和砌圖
設計挑戰問題，採用遊戲和在課堂進行有趣的砌圖，可從三個不同層面去提升學生的解難能力：

1. 創造富有「成功感」的學習環境
在剛開始解難的時候，學生就需要面對困難的難題，他們失敗的機會很大。時常累積的失敗，會引致他們有強烈的挫敗感，失去學習的信心，減低學習的原動力，更會使他們放棄一切學習數學的機會。

反之，若學生從簡單的題目入手，他們得到的成功感，不但幫助他們建立信心，更會令他們有興趣去挑戰較難的題目；雖然他們也有失敗的時候，可是他們之前建立的自信心和成就感，會幫助他們勇於面對困難和解決難題。

2. 建立興趣
活動教學會使課堂教與學較為生活化。篩選合適的課堂活動，會刺激學生和引領他們建立「數學」學習的正面價值觀，提升他們面對難題的適應力，從而積極地去解決數學難題。

3. 營造積極參與的環境
在一個和諧氣氛的學習環境下，學生可以天馬行空地發揮他們的創意，想出一個答案；雖然他們的答案可能和標準答案差異很大，可是在老師不斷的鼓勵和同學的互相扶持下，縱然是很艱深的題目，也可以解決得來。

例二
在一白紙畫有 20 條直線。該 20 條線並沒有兩條或兩條以上是平行的，也沒有三條或三條以上通過同一交點，這 20 條線可構成多少個交點？

讓學生透過分組討論和繪畫，他們不難發現由直線相交而產生的交點，其數目具有特殊的規律。答案可以表列如下：

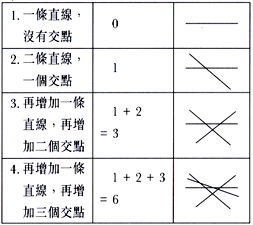
老師可以再提問學生有沒有想到其他的方法。最終，學生發現得到交點的數目和直線的數目可以用柏斯卡（PASCAL）三角形數來表示。

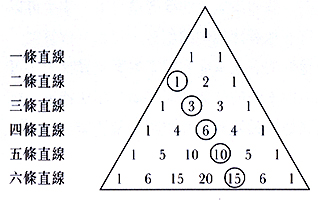
從已知到未知
老師教授學生解難時，必須預留少許彈性和適應性；意念是解題時會使用不同策略和技巧。無論使用哪一種方法，大前題是找出問題的重心和讓問題的答案浮現出來。

例三
一個農夫拿了一籃子雞蛋到市場出售，第一次他賣出全部雞蛋的一半和半隻，第二次他賣出餘下雞蛋的一半和半隻，第三次他賣出餘下雞蛋的一半和半隻；他在第三次出售雞蛋後，他沽清了所有雞蛋。他原來有雞蛋多少隻？

假若學生使用演繹法去尋解，運算的步驟會歸納如下：
設 x 隻為籃子內原有雞蛋的數量。

第一次出售後餘下雞蛋的數量：
x - (0.5x + 0.5) = 0.5x - 0.5

第二次出售後餘下雞蛋的數量：
{0.5x - 0.5 - [0.5 (0.5x - 0.5) + 0.5]}
= 0.25x - 0.75

第三次出售餘下雞蛋的數量：
{0.25x - 0.75 - [0.5 (0.25x - 0.75) + 0.5]}
= 0.125x - 0.875

沽清了雞蛋表示：
0.125x = 0.875
x = 7

從演繹方法得出的結果，會較為繁複。如果使用歸納法時，此一道題比較容易解決。（見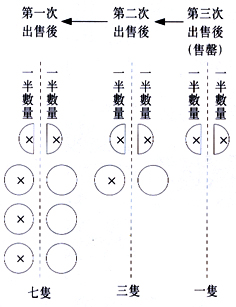圖三）
圖三

籃子內原有雞蛋的數量：
{[(0.5 x 2) + 0.5] x 2 + 0.5} x 2 = 7（隻）

結語
解難的能力需要併入現今數學的課程內，因為無論教育學者、數學教育家、心理學家和老師，都有一個共同的意願：學生必須擁有解難的能力，去面對日後的挑戰。

若果希望提升解難的能力，老師必須豐富學生的創造力，擴闊學生的視野和他們的自信心；好讓學生遇上數學難題時，會有系統的思維方法，對他們日後學習數學，奠下了良好的基礎。

作為一個引導者，老師必須讓學生透過觀察比較，令他們知道可以從多方面去思考數學難題，利用不同方法和使用不同渠道，去尋找最佳解題的路徑。再者，老師若能利用遊戲、有趣的提問或挑戰題和砌圖，都可以讓學生在正面的評價和互相支持的環境中，潛移默化地學習解難的技巧和策略。

最後，學生必須參與解難的訓練和活動，因為他們學習得到的知識，無論在他們的數學學習上，抑或是他們日後面對生活難題上，都有所裨益。