|
傳統的紙筆評估有不少局限之處,近年各國均提出不同方式的「另類評估」(1)。除了評估手段和形式的改變外,更重要是整個評估觀念的改變。早期的評估作用在於「考考你」,有強烈的篩選作用,後來雖轉向學習診斷,仍屬於「評估學習成果」(assessment
of learning)。近年提出「輔翼學習的評估」(assessment
for learning),就是將學習融入評估當中。這其實並不是甚麼嶄新的觀念。以數學科為例,數學題是學習數學的一項核心活動。我們日常佈置不少數學題給學生演練,包括堂課、家課、小測。但傳統上這些練習只發揮兩種作用:一、操練(讓學生熟習有關技巧),二、考察學生是否學會。但這種做法是被動的,較少帶有「學生──教師」的互動性,更難有「學生──題目/數學」之互動。以考察學習成效而言,老師會透過習作、測驗卷等對學生學習情況作出診斷。而至於練習,若果佈置沒有精心策劃,有可能讓學生重複又重複的,愈練愈悶,就是李士錡所說的「熟能生笨」、「熟能心厭」(2)。
但是若我們能在練習題中有系統地引入變化,學生就能透過這些練習題把技巧應用到不同的處境,最終做出靈活運用,觸類旁通。所以練習本身可以是一個很好的學習過程,而它亦可以同時達到學習評估的意味。故此,「評估任務」在真正的促進「學習」(而不是靠評估的威嚇性去作為學習指揮棒的那種「倒流效應」)。學生通過這些「評估」漸漸的學得更多,而變式教學理論對如何在數學題中引進變化提供有用的指導。
為了促進數學教學,中西方分別提出了變異教學理論和變式教學,更有提出「變化」可以提供由基本功變向高層次思維能力的橋樑。筆者等按照這些想法和數學學習之本質,發展了變式課程設計原理。簡單來說是由技巧與數學題的變式歸納出不變的通則,又透過變化,讓學生達至觸類旁通(3)。
要落實這些原理,最重要還是要進行課題上之分析,在適當的地方建築「腳手架」。簡單來說,先分析整個課題之脈絡,再看看哪些是學生較難掌握的環節(所謂「難點」),然後透過由淺入深、循序漸進的變化題,希望學生能較容易掌握。
以中四的「二次方程」為例,課本中涉及了幾個環節,筆者曾作出了分析(4)。現可進一步以圖 1 表示。利用這個分析,我們除了可以看到各課程內容的來龍去脈外,亦可以(當然還要配合教學經驗)認定其中之三個難點。其一是十字相乘法,另一是完全平方法,其三就是二次方程公式。
圖 1 二次方程內容脈絡分析
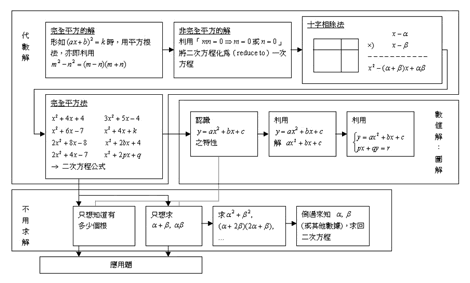
(放大圖片)
對於十字相乘法,慣常手法是「倒過來」看看若能把 x2 + px + q 分解成 (x + a)
(x + b) 。那末,q 一定是 ab,p 一定是
(a + b)。故此問題變成找兩個數,使得其「積 =
q」及其「和 = p」。
順著這個思路,再抽絲剝繭,假若a,b 均是整數就首先試 q 的因數……,在這個環節裡,變式題組已大有可為,這和許多老師慣常的做法一致,就是利用
q 的大細和因數的多少去漸變去形成變式題組如:
x2 + 2x + 1
x2 + 3x + 2
x2 - 3x + 2
x2 + x - 2
x2 + 5x + 6
x2 + 7x - 8
(其後再做一些 x2 系數  1 的)──這其實亦可反過來增強整數及其因數合成的感覺! 1 的)──這其實亦可反過來增強整數及其因數合成的感覺!
至於完全平方法這一環節,題型的變化亦是一種有利之手法,例如從
(x + 3)2 =
9(9是平方數)
到 (x + 4)2 =
7
到 x2 +
4x + 4 = 5
到 x2 +
4x + 4 - 7 = 0
之類。
同理,當學會完全平方法後,可以讓學生用完全平方法分解
x2 +
4x + 4
x2 + 6x -
7
2 x2 + 8x - 8
2 x2 + 4x - 7
3 x2 + 5x - 4
x2 + 4x + k
x2 + 2bx +
4
x2 + 2px + q
等等,就可「自然而然」地引導到二次方程公式。
至於各種應用題,題型分析是常見「有系統地引入變化」的基礎。我們隨意檢出一本本地的教科書,若以上頁的習題為例(見表 1),我們有以上的題型分析(圖2)。 |
|
| 表1 二次方程部分練習題(取自Choi,
P., Chan, W.K. (1981/1986). Certificate amalgamated mathematics.
A modern course (syllabus B), Volume 1. Hong Kong: Chung
Tai Educational Press. 黃民建先生譯成中文) |
|
|
圖 2 二次方程部分練習題中之題型分析
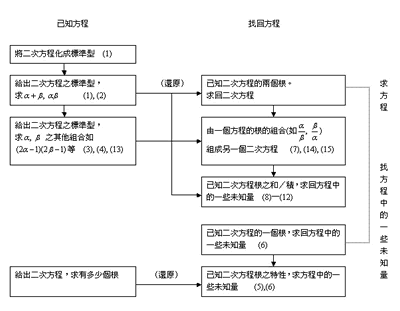
(放大圖片)
當然,我們還得注意這些變式題仍是屬於「入手」的「方便法門」,還要慎防「樣版化」,務使學生能靈活變通。至於「出法」,就要看教師的「開眼」了!
註 (1): |
Fan, L. (2005),
Improving Mathematics Teaching and Learning through Effective Classroom
Assessment: Experiences and Perspectives from Singapore Schools.
In N. Y. Wong, C. K. Leung, & M. Y. Tang (Eds.), Revisiting mathematics
education in Hong Kong for the new Millennium (pp. 359-376). Hong Kong:
Hong Kong Association for Mathematics Education. |
註 (2): |
李士錡(1996),〈熟能生巧嗎〉,《數學教育學報》,5卷3期,頁46-50。;李士錡(1999),〈熟能生笨嗎 — 再談熟能生巧問題〉,《數學教育學報》,8卷3期,頁15-18。;李士錡(2000),〈熟能生厭嗎
— 三談熟能生巧問題〉,《數學教育學報》,9卷2期,頁23-27。 |
註 (3): |
黃毅英、林智中、孫旭花(2006),《變式教學課程設計原理:數學課程改革的可能出路》,香港:香港中文大學教育學院香港教育研究所。 |
註 (4): |
黃毅英(2004),〈其實「二次方程」這一課所講的是甚麼?〉,《進志數學通訊》,3月,頁3-4。 |
|